涨知识 还不知道傅立叶变换的小伙伴快来看看啦

当你们看到傅立叶变换这几个字的时候，你们知道这是什么吗？其实，当小编看到傅立叶变换的时候也不知道它是什么，小编上网搜索之后才对它有了一丢丢的了解，虽然小编了解的还不是那么的透彻，但是小编大体的整理了一下，快来跟小编一起来看看吧！

1、简介

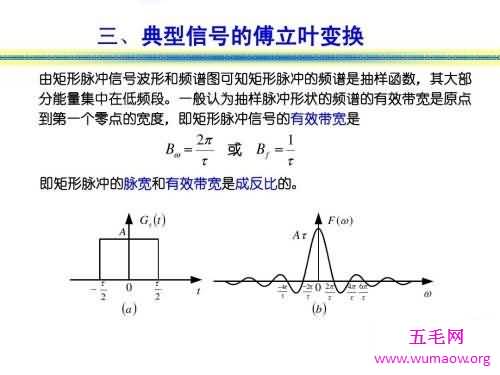
傅立叶变换是一种线性的积分变换，常在将信号在时域（或空域）和频域之间变换时使用，在物理学和工程学中有许多应用。因其基本思想首先由法国学者约瑟夫傅里叶系统地提出，所以以其名字来命名以示纪念。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。

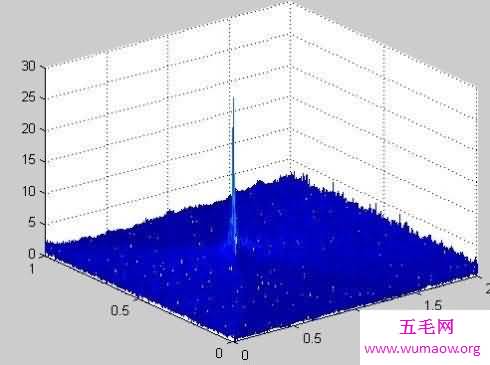
傅里叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。许多波形可作为信号的成分，比如正弦波、方波、锯齿波等，傅里叶变换用正弦波作为信号的成分。

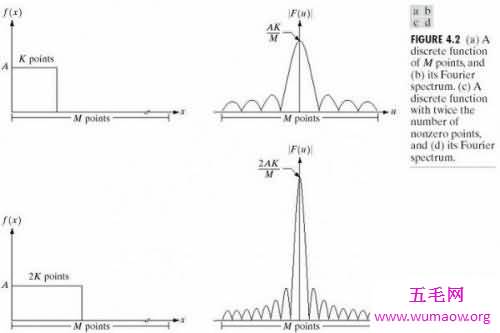
Fourier transform或Transformée de Fourier有多个中文译名，常见的有“傅里叶变换、付立叶变换、傅立叶转换、傅氏转换、傅氏变换、等等。为方便起见，本文统一写作傅里叶变换。傅立叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。许多波形可作为信号的成分，比如正弦波、方波、锯齿波等，傅立叶变换用正弦波作为信号的成分。

2、应用

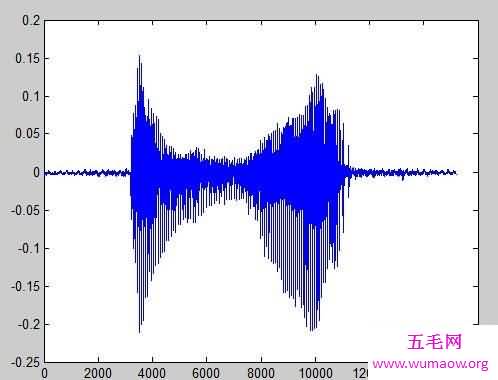
傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用（例如在信号处理中，傅里叶变换的典型用途是将信号分解成幅值谱显示与频率对应的幅值大小）。

3、物理意义

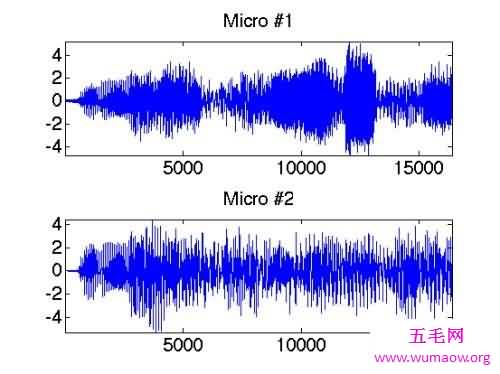
傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理 创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频 率、振幅和相位。

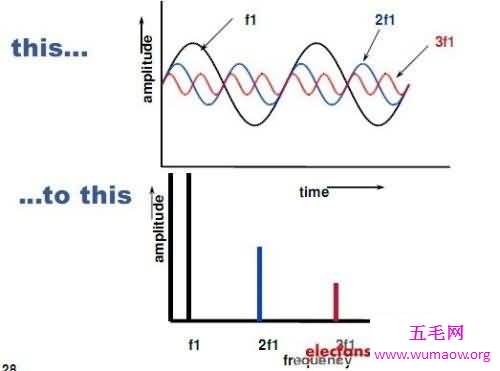
傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号（信号的频谱），可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅立叶反变换将这些频域信号转换成时域信号。

4、性质

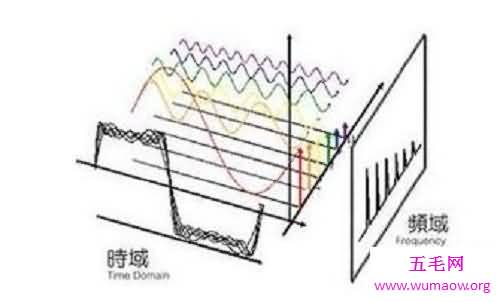
线性性质线性linear，指量与量之间按比例、成直线的关系，在数学上可以理解为一阶导数为常数的函数；非线性non-linear则指不按比例、不成直线的关系，一阶导数不为常数。如问：两个眼睛的视敏度是一个眼睛的几倍？很容易想到的是两倍，可实际是 6－10倍！这就是非线性。

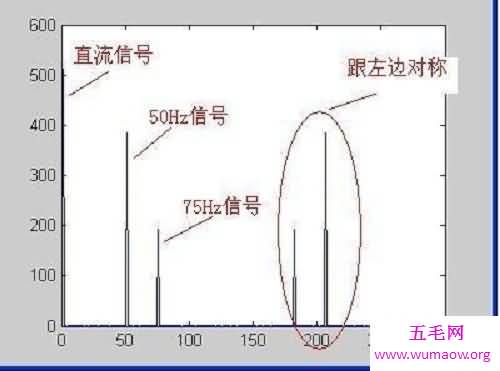
激光也是非线性的！天体运动存在混沌；电、光与声波的振荡，会突陷混沌；地磁场在400万年间，方向突变16次，也是由于混沌。甚至人类自己，原来都是非线性的：与传统的想法相反，健康人的脑电图和心脏跳动并不是规则的，而是混沌的，混沌正是生命力的表现，混沌系统对外界的刺激反应，比非混沌系统快。